EC Cryptography Tutorials - Herong's Tutorial Examples - v1.02, by Dr. Herong Yang
Point Pattern of Reduced Elliptic Curves
This section describes elliptic the repeatable pattern of integer points on reduced elliptic curves. If we know the integer points of the curve in one region, we can move them parallelly to any other region.
In the previous tutorial, we demonstrated how to find integer points on elliptic curves reduced by modular arithmetic of prime numbers p in a single region of (x,y) in {0, 1, 2, ..., p-1}
Element Set in a Single Region:
All P = (x,y), such that:
y2 = x3 + ax + b (mod p)
where:
a and b are integers
p is a prime number
4a3 + 27b2 != 0
x and y are integers in {0, 1, 2, ..., p-1}
Finding integer points the same reduced elliptic curve in other regions is easy. You can just move those points parallelly from the first range to any other region by adding multiples of p to x and y coordinates. You can prove this easily using modular arithmetic properties.
Let's take the same reduced elliptic curve from the previous tutorial of (a,b) = (1,4) and p = 23 as an example:
Reduced Elliptic Curve: y2 = x3 + x + 4 (mod 23)
We found 28 integer points on this curve in the first region:
Points (x,y) on the curve and in the region of {0, 1, 2, ..., 22}
( 0, 2) ( 1,11) ( 4, 7) ( 7, 3) ( 8, 8) ( 9,11) (10, 5)
( 0,21) ( 1,12) ( 4,16) ( 7,20) ( 8,15) ( 9,12) (10,18)
(11, 9) (13,11) (14, 5) (15, 6) (17, 9) (18, 9) (22, 5)
(11,14) (13,12) (14,18) (15,17) (17,14) (18,14) (22,18)
If we want to find integer points in the region of x in {0, 1, 2, ..., 22} and y in {23, 24, 25, ..., 45}, we can just move integer points in the first region by adding 23 to the y coordinates:
Points (x,y) on the curve and in the region
x in {0, 1, 2, ..., 22} and y in {-23, -22, -21, ..., -1}:
( 0,25) ( 1,34) ( 4,30) ( 7,26) ( 8,31) ( 9,34) (10,28)
( 0,44) ( 1,35) ( 4,49) ( 7,43) ( 8,38) ( 9,35) (10,41)
(11,32) (13,34) (14,28) (15,29) (17,32) (18,32) (22,28)
(11,37) (13,35) (14,41) (15,40) (17,37) (18,37) (22,41)
The entire integer 2-dimensional space can be divided into infinite number of such regions. So all integer points on a reduced elliptic curve can be viewed as a single pattern repeats itself in all 4 directions.
Here is a diagram showing this repeatable pattern of integer points on the reduced elliptic curve of (a,b) = (1,4) and p = 23:
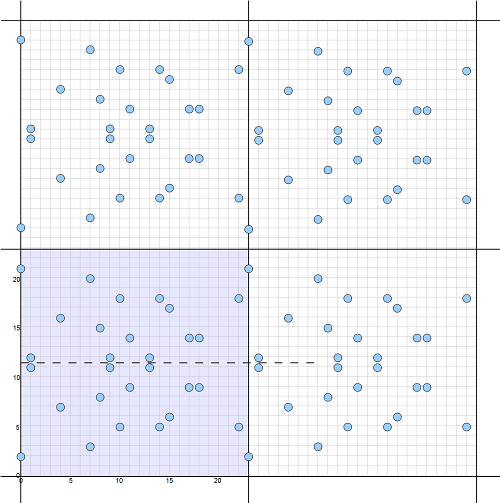
Table of Contents
Geometric Introduction to Elliptic Curves
Algebraic Introduction to Elliptic Curves
Abelian Group and Elliptic Curves
Discrete Logarithm Problem (DLP)
Generators and Cyclic Subgroups
►Reduced Elliptic Curve Groups
Converting Elliptic Curve Groups
Elliptic Curves in Integer Space
Python Program for Integer Elliptic Curves
Elliptic Curves Reduced by Modular Arithmetic
Python Program for Reduced Elliptic Curves
►Point Pattern of Reduced Elliptic Curves
Integer Points of First Region as Element Set
Reduced Point Additive Operation
Modular Arithmetic Reduction on Rational Numbers
Reduced Point Additive Operation Improved
What Is Reduced Elliptic Curve Group
Reduced Elliptic Curve Group - E23(1,4)
Reduced Elliptic Curve Group - E97(-1,1)
Reduced Elliptic Curve Group - E127(-1,3)
Reduced Elliptic Curve Group - E1931(443,1045)
Finite Elliptic Curve Group, Eq(a,b), q = p^n
tinyec - Python Library for ECC
ECDH (Elliptic Curve Diffie-Hellman) Key Exchange
ECDSA (Elliptic Curve Digital Signature Algorithm)