EC Cryptography Tutorials - Herong's Tutorial Examples - v1.03, by Herong Yang
Reduced Elliptic Curve Group - E23(1,4)
This section provides an example of a reduced Elliptic Curve group E23(1,4). A detailed calculation of reduced point doubling operation on (0,2) is also provided.
Let's take a look at our first reduced elliptic curve group, E23(1,4), as discussed in "Implementation Of Elliptic Curve Diffie-Hellman and EC Encryption Schemes by Kefa Rabah at docsdrive.com/pdfs/ansinet/itj/2005/132-139.pdf:
The reduced elliptic curve:
y2 = x3 + x + 4 (mod 23)
The group elements:
( 0, 2) ( 1,11) ( 4, 7) ( 7, 3) ( 8, 8) ( 9,11) (10, 5)
( 0,21) ( 1,12) ( 4,16) ( 7,20) ( 8,15) ( 9,12) (10,18)
(11, 9) (13,11) (14, 5) (15, 6) (17, 9) (18, 9) (22, 5)
(11,14) (13,12) (14,18) (15,17) (17,14) (18,14) (22,18)
( ∞, ∞)
As the first verification case, we can perform the point doubling operation of P = (0,2) again using the reduced additive operation:
Given: P = (xP, yP) = (0, 2) Find: 2P = P + P = R = (xR, yR) Where: xR = m2 - 2xP (mod p) (11) yR = m(xP - xR) - yP (mod p) (12) 2m(yP) = 3(xP)2 + a (mod p) (19) Calculation: 2 * m * 2 = 3 * 0 * 0 + 1 (mod 23) 4 * m = 1 (mod 23) m = 1/4 (mod 23) m = 6 xR = 6*6 - 2*0 = 36 (mod 23) xR = 13 yR = 6*(0 - 13) - 2 = -78 - 2 = -80 (mod 23) yR = 12 Result: 2P = R = (xR, yR) = (13, 12)
Yes, the result of (0,2) + (0,2) = (13, 12) is in the group element set! We Abelian group "Closure" condition is satisfied.
We can also redo the same calculation by using the original equation for the parameter m. We should get the same resulting point:
Given:
P = (xP, yP) = (0, 2)
Find:
2P = P + P = R = (xR, yR)
Where:
xR = m2 - 2xP (mod p) (11)
yR = m(xP - xR) - yP (mod p) (12)
3(xP)2 + a
m = --------- (6)
2(yP)
Calculation:
m = (3*0*0 + 1)/(2*2) = 1/4
xR = (1/4)*(1/4) - 2*0 = 1/16 (mod 23)
xR = 13
xR = (1/4)*(0 - 1/16) - 2 = -1/64 - 2 = -129/64 (mod 23)
xR = 9 * 1/18 (mod 23) = 9 * 9 (mod 23)
xR = 12
Result:
2P = R = (xR, yR) = (13, 12)
Cool. This demonstrates that keep m as a rational number without modular reduction is also provides the same resulting point.
Here is a diagram of all non-infinite points of the E23(1,4) group:
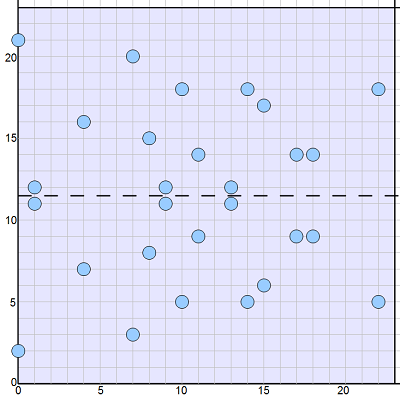
Table of Contents
Geometric Introduction to Elliptic Curves
Algebraic Introduction to Elliptic Curves
Abelian Group and Elliptic Curves
Discrete Logarithm Problem (DLP)
Generators and Cyclic Subgroups
►Reduced Elliptic Curve Groups
Converting Elliptic Curve Groups
Elliptic Curves in Integer Space
Python Program for Integer Elliptic Curves
Elliptic Curves Reduced by Modular Arithmetic
Python Program for Reduced Elliptic Curves
Point Pattern of Reduced Elliptic Curves
Integer Points of First Region as Element Set
Reduced Point Additive Operation
Modular Arithmetic Reduction on Rational Numbers
Reduced Point Additive Operation Improved
What Is Reduced Elliptic Curve Group
►Reduced Elliptic Curve Group - E23(1,4)
Reduced Elliptic Curve Group - E97(-1,1)
Reduced Elliptic Curve Group - E127(-1,3)
Reduced Elliptic Curve Group - E1931(443,1045)
Finite Elliptic Curve Group, Eq(a,b), q = pn
tinyec - Python Library for ECC
ECDH (Elliptic Curve Diffie-Hellman) Key Exchange
ECDSA (Elliptic Curve Digital Signature Algorithm)