EC Cryptography Tutorials - Herong's Tutorial Examples - v1.03, by Herong Yang
Reduced Elliptic Curve Group - E1931(443,1045)
This section provides an example of a reduced Elliptic Curve group E1931(443,1045).
Let's take a look at another reduced elliptic curve group, E1931(433,1045), as discussed in "2018 Math Summer Camp - Explicit construction of elliptic curves with prescribed order over finite fields" at mathduc.com/summercamp/.
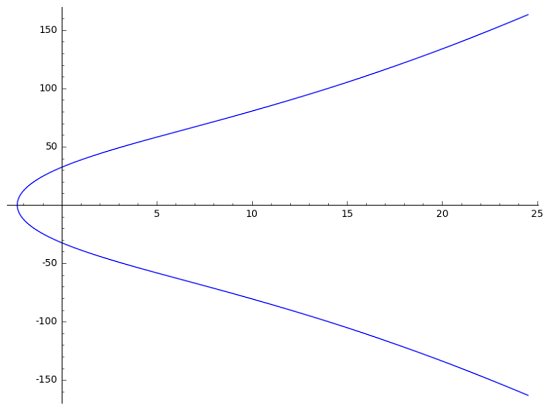
Here is the elliptic curve in the real number space:
y2 = x3 - 443x + 1045
Here is the reduced elliptic curve group using modular arithmetic of prime number 1931, E1931(443,1045):
y2 = x3 - 443x + 1045 (mod 1931)
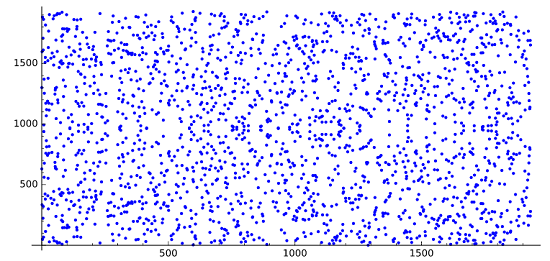
As you can see, there are a lots of elements in a reduced elliptic curve group, when a large prime number is used. Is there any formula to calculate the number of elements (also called the order) of an a reduced elliptic curve group? We will discuss it in the next tutorial.
Table of Contents
Geometric Introduction to Elliptic Curves
Algebraic Introduction to Elliptic Curves
Abelian Group and Elliptic Curves
Discrete Logarithm Problem (DLP)
Generators and Cyclic Subgroups
►Reduced Elliptic Curve Groups
Converting Elliptic Curve Groups
Elliptic Curves in Integer Space
Python Program for Integer Elliptic Curves
Elliptic Curves Reduced by Modular Arithmetic
Python Program for Reduced Elliptic Curves
Point Pattern of Reduced Elliptic Curves
Integer Points of First Region as Element Set
Reduced Point Additive Operation
Modular Arithmetic Reduction on Rational Numbers
Reduced Point Additive Operation Improved
What Is Reduced Elliptic Curve Group
Reduced Elliptic Curve Group - E23(1,4)
Reduced Elliptic Curve Group - E97(-1,1)
Reduced Elliptic Curve Group - E127(-1,3)
►Reduced Elliptic Curve Group - E1931(443,1045)
Finite Elliptic Curve Group, Eq(a,b), q = pn
tinyec - Python Library for ECC
ECDH (Elliptic Curve Diffie-Hellman) Key Exchange
ECDSA (Elliptic Curve Digital Signature Algorithm)