Physics Notes - Herong's Tutorial Notes - v3.25, by Herong Yang
3-Dimensional Cartesian Coordinate System
This section provides an introduction of 3-dimensional Cartesian coordinate systems, which uses perpendicular projections on 3 perpendicular axes to describe any locations in the frame of reference.
If we want to describe locations of a space shuttle flying towards a space station, we need a 3-dimensional frame of reference and an associated coordinate system.
First, let's define a 3-dimensional frame of reference with the following reference points:
- First reference point - The center of Earth.
- Second reference point - The intersection point of the Equator Plane and the Prime Meridian plane.
- Third reference point - The North Pole.
Next, let's define a 3-dimensional Cartesian coordinate system and associate it to the above frame of reference:
- Set the origin of the Cartesian coordinate system at the center of Earth.
- Set the x-axis along the straight line from the center of Earth to the intersection point of the Equator Plane and the Prime Meridian Plane. Scale the x-axis with 1 km per unit.
- Set the z-axis along the straight line from the center of Earth to the North Pole. Scale the z-axis with 1 km per unit.
- Set the y-axis along the straight line passing through the center of Earth and perpendicular to the Prime Meridian Plane. Scale the y-axis with 1 km per unit.
Now we are can describe any location of the space shuttle while it's flying as a set of 3 coordinate numbers.
For example, the location of the space shuttle shown in the picture below can be described as (19113, 20706, 11857), because:
- Its perpendicular projection on the x-axis is 19,113 km.
- Its perpendicular projection on the y-axis is 20,706 km.
- Its perpendicular projection on the z-axis is 11,857 km.
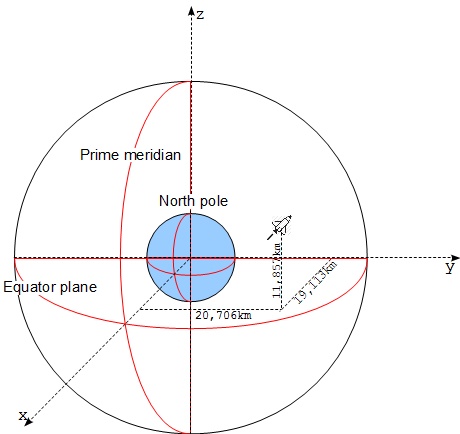
Table of Contents
►Introduction of Frame of Reference
Frame of Reference with 2 Objects
2-Dimensional Cartesian Coordinate System
►3-Dimensional Cartesian Coordinate System
1 Frame of Reference with 2 Coordinate Systems
Introduction of Special Relativity
Time Dilation in Special Relativity
Length Contraction in Special Relativity
The Relativity of Simultaneity
Minkowski Spacetime and Diagrams
Introduction of Generalized Coordinates