Physics Notes - Herong's Tutorial Notes - v3.25, by Herong Yang
2-Dimensional Cartesian Coordinate System
This section provides an introduction of 2-dimensional Cartesian coordinate systems, which uses perpendicular projections on 2 perpendicular axes to describe any locations in the frame of reference.
When describing an object that is moving along non-straight line, we need to use 2-dimensional or 3-dimensional frame of references and coordinate systems.
For example, the trajectory of a flying golf ball is not a straight line, but it can described with a 2-dimensional frame of reference and an associated coordinate system.
First, let's define a 2-dimensional frame of reference as a vertical rectangle:
- The first edge runs from the golf ball stand to target hole.
- The second edge runs from the golf ball stand straight up to the sky for 10 meters.
- The third edge runs from the target hole straight up to the sky for 10 meters.
- The last edge connects the end point of the second edge and the first edge.
Next, let's create a simple coordinate system:
- Set a 2-dimensional Cartesian coordinate system on the frame of reference.
- Set the origin of the Cartesian coordinate system at the golf ball stand.
- Set the x-axis along the first edge of the frame of reference. Scale the x-axis with 1 meter per unit.
- Set the y-axis along the second edge of the frame of reference. Scale the x-axis with 1 meter per unit.
Now we are can describe any location of the golf ball while it's flying in the air as a pair of coordinate numbers by reading scales of its perpendicular projections on the x-axis and the y-axis.
For example, the highest location of the golf ball in the picture below can be described as (14.89, 7.93) because:
- Its perpendicular projection on the x-axis is 14.89 meters.
- Its perpendicular projection on the y-axis is 7.93 meters.
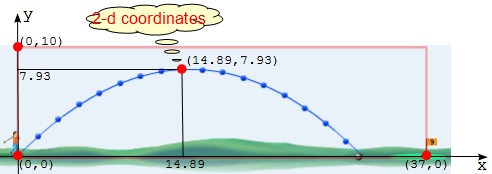
Table of Contents
►Introduction of Frame of Reference
Frame of Reference with 2 Objects
►2-Dimensional Cartesian Coordinate System
3-Dimensional Cartesian Coordinate System
1 Frame of Reference with 2 Coordinate Systems
Introduction of Special Relativity
Time Dilation in Special Relativity
Length Contraction in Special Relativity
The Relativity of Simultaneity
Minkowski Spacetime and Diagrams
Introduction of Generalized Coordinates