1 Frame of Reference with 2 Coordinate Systems

∟1 Frame of Reference with 2 Coordinate Systems

This section provides an example of a frame of reference associated with 2 coordinate systems. The location of an object can be described as 2 sets of coordinates.

A single frame of reference can be associated with multiple coordinate systems. In this case, the location of an object in the same frame of reference will have different sets of coordinates depending on which coordinate system is used.

For example, we can define a sphere coordinate system and associate it to the same frame of reference presented in the previous section:

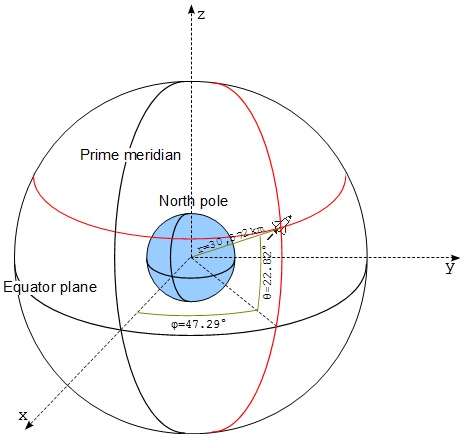
Set the origin of the sphere coordinate system at the center of Earth.
Set the x-axis along the straight line from the center of Earth to the intersection point of the Equator Plane and the Prime Meridian Plane.
Set the φ (phi) angle on the Equator plane relative to the x-axis.
Set the θ (theta) angle on any meridian plane relative to the its intersection with the Equator plane.
Set the r (radius) distance along the straight line from the center of Earth to the location of the object. Scale the r distance with 1 km per unit.

Now we describe the same location of the space shuttle in this new sphere coordinate system as (47.29, 22.82, 30572), because:

Its perpendicular projection on the Equator plane has a φ angle of 47.29°.
Its radius on the meridian plane on a θ angle of 22.82°.
Its radius is 30,572 km.

1 Frame of Reference with 2 Coordinate Systems

Note that the φ angle is also called Longitude, the θ angle is also called Latitude, and the r distance minus Earth radius (6,371km) is also called Altitude. So the location of the space shuttle can also be described:

Longitude = 47.29°
Latitude = 22.82°
Altitude = 24,201km

Table of Contents

About This Book

Introduction of Space

►Introduction of Frame of Reference

What Is Frame of Reference

Frame of Reference with 2 Objects

What Is Coordinate System

2-Dimensional Cartesian Coordinate System

3-Dimensional Cartesian Coordinate System

►1 Frame of Reference with 2 Coordinate Systems

Introduction of Time

Introduction of Speed

Newton's Laws of Motion

Introduction of Special Relativity

Time Dilation in Special Relativity

Length Contraction in Special Relativity

The Relativity of Simultaneity

Introduction of Spacetime

Minkowski Spacetime and Diagrams

Introduction of Hamiltonian

Introduction of Lagrangian

Introduction of Generalized Coordinates

Phase Space and Phase Portrait

References

Full Version in PDF/ePUB