Physics Notes - Herong's Tutorial Notes

∟Phase Space and Phase Portrait

∟What Is Phase Portrait

This section provides an introduction to Phase Portrait, which is the trajectory curve of a system in the the Phase Space for a given period of time.

What Is Phase Portrait? Phase Portrait is the trajectory curve of a system in the the Phase Space for a given period of time.

For a single-object system with 1 degree of freedom, the Phase Space is a 2 dimensional space of (q₁, p₁). In this case, the Phase Portrait becomes a 2 dimensional curve.

Phase Portrait of Free Fall Motion

Let's take a look at Phase Portrait of the Free Fall Motion of a single object with mass m. In this case, the generalized position has only 1 component x, representing the height of the object. So we can express Canonical Coordinates (q,p) of the system as below:

q = (x)
p = (m*x')
  # x is the height of the object
  # m is the mass of the object
  # x' is the velocity of the object

The Hamilton Function can be expressed as:

H = T + V 

or: 
  H = p*p/(2m) + m*g*q                  (P.1)
    # g is the standard gravity (9.80665)

If we apply Hamilton Equations, we have:

∂H/∂q = -p'                                (P.2) 
∂H/∂p = q'                                 (P.3)

or: 
  ∂(p*p/(2m) + m*g*q)/∂q = -p'
  ∂(p*p/(2m) + m*g*q)/∂p = q'

or: 
  m*g = -p'                             (P.4)
  p/m = q'                              (P.5)

Equations P.4 and P.5 are the equations of the free fall motion, which has the following solution:

q(t) = -g*t*t/2 + p0*t + q0
p(t) = -m*g*t + p0
  # q0 is the initial position
  # p0 is the initial momentum

The Phase Portrait of this system is a parabolic curve in the Phase Plane of (q,p). For example, if the system has a initial condition of (q,p) = (0,1), its Phase Portrait will look like this:

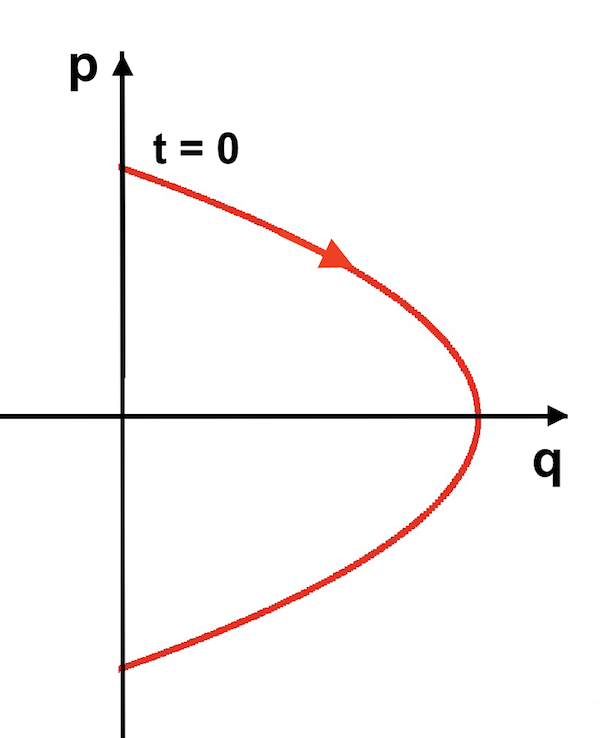
Table of Contents

 About This Book

 Introduction of Space

 Introduction of Frame of Reference

 Introduction of Time

 Introduction of Speed

 Newton's Laws of Motion

 Introduction of Special Relativity

 Time Dilation in Special Relativity

 Length Contraction in Special Relativity

 The Relativity of Simultaneity

 Introduction of Spacetime

 Minkowski Spacetime and Diagrams

 Introduction of Hamiltonian

 Introduction of Lagrangian

 Introduction of Generalized Coordinates

►Phase Space and Phase Portrait

 What Is Phase Space

►What Is Phase Portrait

 Phase Portrait of Simple Harmonic Motion

 Phase Portrait of Pendulum Motion

 Motion Equations of Linear Systems

 Phase Portraits of 2-D Homogeneous Linear Systems

 References

 Full Version in PDF/ePUB

What Is Phase Portrait - Updated in 2022, by Herong Yang