Phase Portrait of Simple Harmonic Motion

∟Phase Portrait of Simple Harmonic Motion

This section provides phase portrait examples for a single object in simple harmonic motion.

Now let's look the Phase Portrait of a single object in Simple Harmonic Motion.

If we consider an object of mass m on a spring moving horizontally on a frictionless surface, the generalized position can be set to the displacement x from the equilibrium position. So we can express Canonical Coordinates (q,p) of the system as below:

q = (x)
p = (m*x')
  # x is object's displacement
  # m is the mass of the object
  # x' is the velocity of the object

The Hamilton Function can be expressed as:

H = T + V 

or: 
  H = p*p/(2m) + k*q*q/2                (P.6)
    # k is the spring constant

If we apply Hamilton Equations, we have:

∂H/∂q = -p'                                (P.2) 
∂H/∂p = q'                                 (P.3)

or: 
  ∂(p*p/(2m) + k*q*q/2)/∂q = -p'   
  ∂(p*p/(2m) + k*q*q/2)/∂p = q'

or: 
  kq = -p'                              (P.7)
  p/m = q'                              (P.8)

Equations P.7 and P.8 are the equations of the free fall motion, which has the following solution:

q(t) =  A*    cos(w*t - u)
p(t) = -A*w*m*sin(w*t - u)
  # A is the amplitude (maximum displacement)
  # w = sqrt(k/m), is the angular frequency
  # u is the initial phase

The Phase Portrait of this system is an ellipse in the Phase Plane of (q,p). It centers at the origin of (q,p) = (0,0).

If we start the system by pushing the object to different displacement positions and release it with zero speed, we will get different moving patterns of the system, which will result different Phase Portraits on the phase plane as shown below (source: researchgate.net).

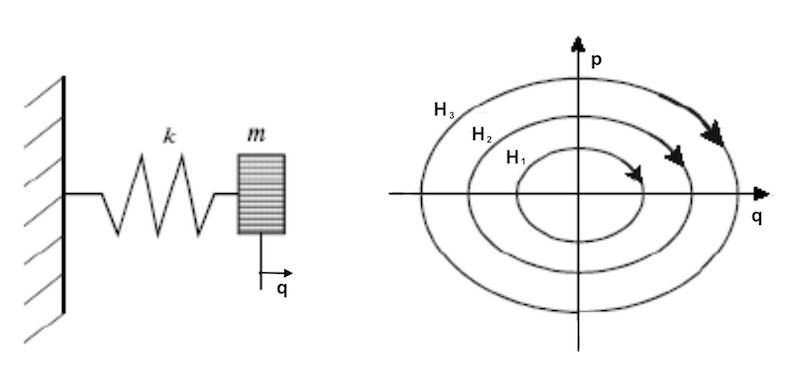
Phase Portrait for Simple Harmonic Motion

Actually, for a conservative system, the Hamiltonian Function on each Phase Portrait has a constant value. In other words, Phase Portraits are Hamiltonian contours in the Phase Space.