Hamiltonian on Simple Harmonic Motion

∟Hamiltonian on Simple Harmonic Motion

This section provides an example of calculating the Hamiltonian on a mechanical system of an single object in simple harmonic motion and applying the Law of Conservation of Energy.

What Is Simple Harmonic Motion? Simple Harmonic Motion is a periodic motion where the restoring force on the moving object is directly proportional to the magnitude of the object's displacement and acts towards the object's equilibrium position.

Let's first consider a mass on a spring moving horizontally on a frictionless surface as an example of Simple Harmonic Motion. The object's kinetic energy, T, and potential energy, V, can be expressed as:

T = m*v*v/2
  # m is the mass of the object
  # v is the velocity of the object

V = k*x**2/2
  # k is the spring constant
  # x is object's displacement from the equilibrium position

So the Hamiltonian, H, of the free fall motion system can be expressed as:

H = T + V

or:
  H = m*v*v/2 + k*x**2/2

Since this simple harmonic motion can be considered as an isolated conservative system, we can apply the Law of Conservation of Energy:

H = constant

or:
  m*v*v/2 + k*x**2/2 = constant

or:
  d(m*v*v/2)/dt + d(k*x**2/2)/dt = 0
    # Since d(constant)/dt = 0

The last equation can be simplified as:

d(m*v*v/2)/dt + d(m*k*x)/dt = 0

m*v*dv/dt + k*x*dx/dt = 0
  # The chain rule for derivatives applied

m*v*a + k*x*v = 0
  # a = dv/dt, is the acceleration of the object
  # v = dx/dt, is the velocity of the object

m*a + k*x = 0
m*a = -k*x                         (H.6)
  # Cancel out v from the equation

Cool. Equation H.6 matches perfectly with Newton's second law of motion:

F = m*a                            (H.5)
  # Newton's second law of motion

-k*x = m*a
  # Hooke's law, F = -k*x, applied.

m*a = -k*x                         (H.6)
  # Moving terms around

With equation H.6, we can figure out the position x, the velocity v, and the acceleration a, as functions of time t. This is done by introducing some other constants:

x(t) =  A*    cos(w*t - u)
v(t) = -A*w*  sin(w*t - u)
a(t) = -A*w*w*cos(w*t - u)
  # A is the amplitude (maximum displacement)
  # w = sqrt(k/m), is the angular frequency
  # u is the initial phase

The following picture illustrates an object on a spring moving horizontally (source: slideserver.com):

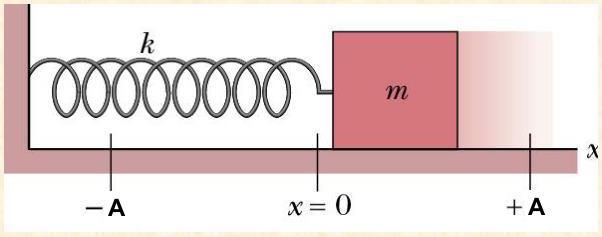
By the way, calculating Hamiltonian and applying the Law of Conservation of Energy to an object on a spring moving vertically results the same equation. The only difference is that the object's displacement, x, is pointing vertically.

m*a = -k*x                         (H.6)

The following picture illustrates an object on a spring moving vertically (source: wikipedia.org):

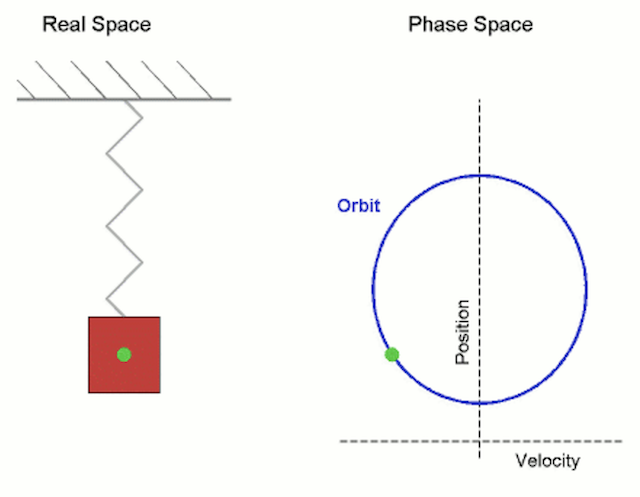
Table of Contents

About This Book

Introduction of Space

Introduction of Frame of Reference

Introduction of Time

Introduction of Speed

Newton's Laws of Motion

Introduction of Special Relativity

Time Dilation in Special Relativity

Length Contraction in Special Relativity

The Relativity of Simultaneity

Introduction of Spacetime

Minkowski Spacetime and Diagrams

►Introduction of Hamiltonian

What Is Hamiltonian

Hamiltonian on Free Fall Motion

►Hamiltonian on Simple Harmonic Motion

Hamiltonian on Simple Pendulum Motion

What Is Momentum

Relation of Momentum and Hamiltonian

Hamiltonian in Cartesian Coordinates

Relation of Momentum and Potential Energy

Hamilton Equations in Cartesian Coordinates

Introduction of Lagrangian

Introduction of Generalized Coordinates

Phase Space and Phase Portrait

References

Full Version in PDF/ePUB