Physics Notes - Herong's Tutorial Notes - v3.25, by Herong Yang
Hamiltonian on Simple Pendulum Motion
This section provides an example of calculating the Hamiltonian on a mechanical system of an single object in simple pendulum motion and applying the Law of Conservation of Energy.
What Is Simple Pendulum Motion? A Simple Pendulum Motion is an object of mass m hanging on a string from a pivot point so that it is constrained to move on a circle of a fixed radius.
If we map the space in Cartesian coordinates, the Simple Pendulum Motion is a 2-dimensional problem, both the position, r, and the speed, v, have 2 components:
r = (x, y) v = (x', y')
If we introduce an extra variable θ as the angular position of the object from the vertical line, r and v can be expressed as:
r = (l*sin(θ), -l*cos(θ)) v = (l*cos(θ)*θ', l*sin(θ)*θ')
Now the object's kinetic energy, T, can be expressed as:
T = m*|v|**2 or: T = 0.5*m*l*l*(cos(θ)**2)+sin(θ)**2)*θ'*θ' # Pythagorean Theorem applied or: T = 0.5*m*l*l*θ'*θ' # Since cos(θ)**2)+sin(θ)**2 = 1
The potential energy, V, can be expressed as:
V = m*g*y or: V = m*g*(-l*cos(θ)) or: V = -m*g*l*cos(θ)
So the Hamiltonian, H, can be expressed as:
H = T + V (H.1)
or:
H = 0.5*m*l*l*θ'*θ' - m*g*l*cos(θ)
# Replaced T and V with their expressions
Since this simple pendulum motion can be considered as an isolated conservative system, we can apply the Law of Conservation of Energy:
H = constant or: 0.5*m*l*l*θ'*θ' - m*g*l*cos(θ) = constant or: d(0.5*m*l*l*θ'*θ' - m*g*l*cos(θ))/dt = 0 # Since d(constant)/dt = 0 or: m*l*l*θ'*θ" + m*g*l*sin(θ)*θ' = 0 l*θ" + g*sin(θ) = 0 θ" = - g*sin(θ)/l
Cool. We got the simplest form of the equations for the simple pendulum motion.
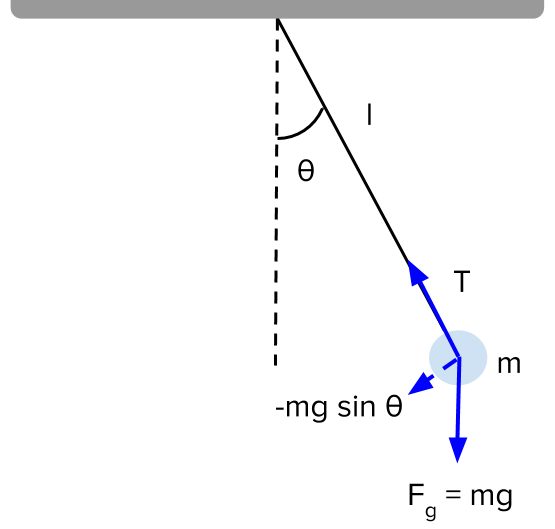
Table of Contents
Introduction of Frame of Reference
Introduction of Special Relativity
Time Dilation in Special Relativity
Length Contraction in Special Relativity
The Relativity of Simultaneity
Minkowski Spacetime and Diagrams
Hamiltonian on Free Fall Motion
Hamiltonian on Simple Harmonic Motion
►Hamiltonian on Simple Pendulum Motion
Relation of Momentum and Hamiltonian
Hamiltonian in Cartesian Coordinates
Relation of Momentum and Potential Energy
Hamilton Equations in Cartesian Coordinates
Introduction of Generalized Coordinates