Physics Notes - Herong's Tutorial Notes - v3.22, by Dr. Herong Yang
What Is Minkowski Diagram?
This section provides an introduction of Minkowski diagram, which represents the Lorentz Transformation overlaying a moving frame into a stationary frame.
What Is Minkowski Diagram? Minkowski diagram is a spacetime diagram that overlays a moving frame into a stationary frame to represent Lorentz Transformation in a geometric model.
Using the same thought experiment in the previous section as an example, the Minkowski diagram from Bob's point of view can constructed as below:
- Draw an orthogonal coordinate system of (x,ct) to represent Bob's frame.
- Draw the ct' axis of Amy's frame along the worldline of Amy's location.
- Draw the x' axis of Amy's frame by flipping ct' axis against the light cone line.
- Scale ct' as (sqrt(1+(v/c)**2)/sqrt(1-(v/c)**2))*ct.
- Scale x' as (sqrt(1+(v/c)**2)/sqrt(1-(v/c)**2))*x.
For a given event E=(X,cT), the (X',cT') coordinates calculated by the Lorentz Transformation can be read from the Minkowski diagram geometrically:
- Draw a point E at (X,cT) in Bob's frame.
- Read X' value on x' axis by projecting E along ct' to x'
- Read cT' value on ct' axis by projecting E along x' to ct'
For example, assuming the train is moving at the speed of 0.6*c, an event E at (X,cT)=(5.5,6.5) on Bob's light cone would be observed by Bob in Amy's frame as (X',cT')=(2,4) based on Lorentz transformation.
The following picture shows a Minkowski diagram of the above example produced by the interactive Minkowski diagram tool at http://www.trell.org/div/minkowski.html:
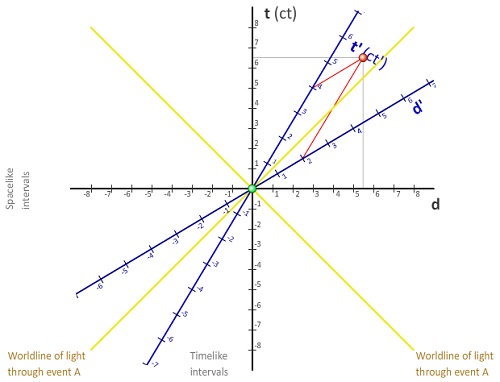
Table of Contents
Introducion of Frame of Reference
Introduction of Special Relativity
Time Dilation in Special Relativity
Length Contraction in Special Relativity
The Relativity of Simultaneity
►Minkowski Spacetime and Diagrams
What Is Lorentz Transformation?
Constancy of Speed of Light in Minkowski Diagram
Time Dilation in Minkowski Diagram
Length Contraction in Minkowski Diagram
Relativity of Simultaneity in Minkowski Diagram
Invariant Spacetime Interval in Minkowski Diagram