Physics Notes - Herong's Tutorial Notes - v3.22, by Dr. Herong Yang
What Is Lorentz Transformation?
This section provides an introduction of Lorentz Transformation, which maps coordinates of an event in a stationary frame to a moving frame under the special theory of relativity.
Now we can look at the second contribution from Hermann Minkowski in constructing a geometric model called Minkowski diagram to support the special theory of relativity. Minkowski diagram is closely related to Lorentz Transformation. So let's start with the Lorentz Transformation first.
What Is Lorentz Transformation? Lorentz Transformation is a transformation formula that maps coordinates of an event in a stationary frame to a moving frame under the special theory of relativity.
We can use the moving train thought experiment to present a simplified version of Lorentz Transformation:
- Bob on the ground uses the ground as his reference frame (x,ct), where x is the space coordinate and ct is the time coordinate scaled by the speed of light c. In order to simplify the discussion, only 1-dimension space is considered.
- Amy on a moving train uses the train as her reference frame (x',ct'), where x' is the space coordinate and ct' is the time coordinate scaled by the speed of light c.
- The origin of (x',ct') is adjusted to be at the same location as the origin of (x,ct). That is, we have (x',ct') = (0,0) when (x,ct) = (0,0).
- The train is moving at a constant speed of v relative to the ground.
For the above example, the Lorentz Transformation for a given event E from Bob's point of view can be expressed as below:
X' = gamma*( X - beta*c*T) #3: Lorentz Transformation c*T' = gamma*(-beta*X + c*T) #4: Lorentz Transformation # Observed from Bob's stationary frame where: (X',cT') #5: Event E in Amy's frame (X,cT) #6: Event E in Bob's frame gamma = 1/sqrt(1-beta**2) #7: "gamma" factor beta = v/c #8: "beta" factor
For example, assuming the train is moving at the speed of 0.6*c, an event E at (X,cT)=(5.5,6.5) on Bob's light cone would be observed by Bob in Amy's frame as (X',cT')=(2,4) based on Lorentz transformation #3 and #4.
beta = v/c = 0.6*c/c = 0.6 gamma = 1/sqrt(1-beta**2) = 1.25 X' = 1.25*( 5.5 - 0.6*6.5) #9: from #3 c*T' = 1.25*(-0.6*5.5 + 6.5) #10: from #4 X' = 2 #11: from #9 c*T' = 4 #12: from #10
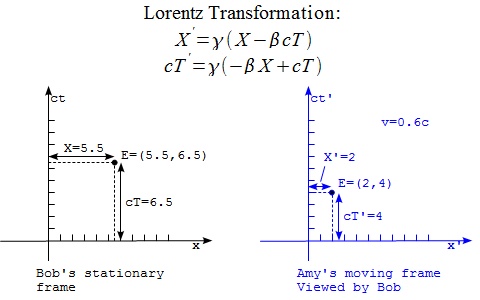
Table of Contents
Introducion of Frame of Reference
Introduction of Special Relativity
Time Dilation in Special Relativity
Length Contraction in Special Relativity
The Relativity of Simultaneity
►Minkowski Spacetime and Diagrams
►What Is Lorentz Transformation?
Constancy of Speed of Light in Minkowski Diagram
Time Dilation in Minkowski Diagram
Length Contraction in Minkowski Diagram
Relativity of Simultaneity in Minkowski Diagram
Invariant Spacetime Interval in Minkowski Diagram