Physics Notes - Herong's Tutorial Notes - v3.22, by Dr. Herong Yang
What Is Minkowski Spacetime?
This section provides a quick introduction on Minkowski spacetime, a 4-dimentional spacetime coordinate system used with a frame of reference to mathematically describe the special theory of relativity.
What Is Minkowski Spacetime?? Minkowski spacetime is a 4-dimentional spacetime coordinate system named after the mathematician Hermann Minkowski. Minkowski spacetime is the most convenient coordinate system used with a frame of reference to mathematically describe the special theory of relativity.
Minkowski spacetime has the following main assumptions:
4 axes (t,x,y,z) are mutually orthogonal.
The distance (or interval), s, between two points (or events) is defined as:
s = sqrt(-(c*dt)**2+dx**2+dy**2+dz**2) #1: Minkowski interval # c is the speed of light # dt, dx, dy, and dz are coordinate differences of the two points
Notice that the time component has a negative sign different than space components in the definition. This is an important contribution from Hermann Minkowski in constructing spacetime mathematical models. Distance is no longer a non-negative number. It is not even a real number in case where (c*dt)**2 > (dx**2+dy**2+dz**2).
If we simplify a Minkowski spacetime by dropping y and z dimensions and scale the time axis as c*t, we can illustrate the interval of two events as shown in the diagram below:
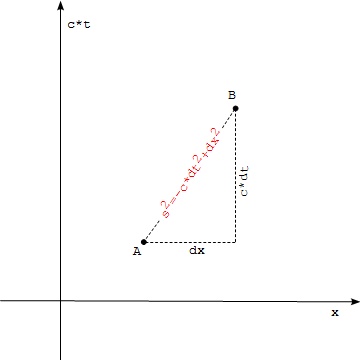
Table of Contents
Introducion of Frame of Reference
Introduction of Special Relativity
Time Dilation in Special Relativity
Length Contraction in Special Relativity
The Relativity of Simultaneity
►Minkowski Spacetime and Diagrams
What Is Lorentz Transformation?
Constancy of Speed of Light in Minkowski Diagram
Time Dilation in Minkowski Diagram
Length Contraction in Minkowski Diagram
Relativity of Simultaneity in Minkowski Diagram
Invariant Spacetime Interval in Minkowski Diagram