EC Cryptography Tutorials - Herong's Tutorial Examples - v1.02, by Dr. Herong Yang
Same Point Addition on an Elliptic Curve
This section describes how to perform the addition operation of a point P to the same point P on an elliptic curve. In this case, we will draw a straight line that passes P and tangent to the curve to find -R.
What happens if we want add a point P on an elliptic curve to itself?
In this case, we need to modify our geometrical algorithm as the following to find R:
1. Draw a straight line passing P and tangent to the elliptic curve.
2. Mark the second intersection of the straight line and the elliptic curve as -R.
3. Mark the symmetrical point of -R on the other side of the x-axis of the elliptic curve as R.
If we use the plus sign "+" as the addition operator, the addition operation of a point P to itself on an elliptic curve can be expressed as:
P + P = R
The above expression can abbreviated as the following, if we follow algebraic formula convention:
P + P = 2P = R
Here is a diagram that illustrates how to perform the addition operation on an elliptic curve geometrically (source: hackernoon.com):
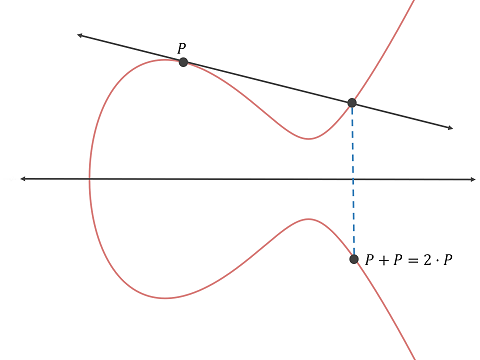
Table of Contents
►Geometric Introduction to Elliptic Curves
Elliptic Curve Geometric Properties
Addition Operation on an Elliptic Curve
Prove of Elliptic Curve Addition Operation
►Same Point Addition on an Elliptic Curve
Infinity Point on an Elliptic Curve
Negation Operation on an Elliptic Curve
Subtraction Operation on an Elliptic Curve
Identity Element on an Elliptic Curve
Commutativity of Elliptic Curve Operations
Associativity of Elliptic Curve Operations
Elliptic Curve Operation Summary
Algebraic Introduction to Elliptic Curves
Abelian Group and Elliptic Curves
Discrete Logarithm Problem (DLP)
Generators and Cyclic Subgroups
tinyec - Python Library for ECC
ECDH (Elliptic Curve Diffie-Hellman) Key Exchange
ECDSA (Elliptic Curve Digital Signature Algorithm)