EC Cryptography Tutorials - Herong's Tutorial Examples - v1.03, by Herong Yang
Infinity Point on an Elliptic Curve
This section describes how the infinity point is used to represent the intersection of vertical lines and elliptic curves.
In order to completely define the addition operation on an elliptic curve, we need to introduce a special point on the curve, the infinity point.
Consider the following addition operation of P and Q on an elliptic curve, where Q is the symmetrical point of P on the same curve. Or we can express Q as:
Q = -P
In this case, we can follow our geometrical algorithm to find the R = P + Q:
1. Draw a straight line passing P and -P. This will be a vertical line.
2. Mark the third intersection of the vertical line and the elliptic curve as -R, which will be the infinity point of the 2-dimensional space. This is where the vertical line and the elliptic curve will eventually intersect. In other words, -R is the infinity point:
-R = (∞, ∞)
3. Mark the symmetrical point of -R on the other side of the x-axis of the elliptic curve as R which will be the same infinity point. This is because the infinity point has no difference between positive or negative signs. In other words, R is the infinity point:
R = (∞, -∞) = (∞, ∞)
Here is a diagram that illustrates how a vertical line intersects with an elliptic curve at the infinity point.
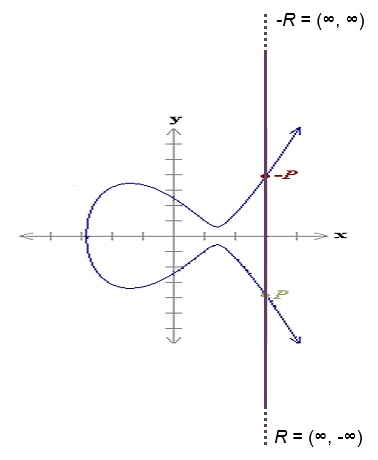
Table of Contents
►Geometric Introduction to Elliptic Curves
Elliptic Curve Geometric Properties
Addition Operation on an Elliptic Curve
Prove of Elliptic Curve Addition Operation
Same Point Addition on an Elliptic Curve
►Infinity Point on an Elliptic Curve
Negation Operation on an Elliptic Curve
Subtraction Operation on an Elliptic Curve
Identity Element on an Elliptic Curve
Commutativity of Elliptic Curve Operations
Associativity of Elliptic Curve Operations
Elliptic Curve Operation Summary
Algebraic Introduction to Elliptic Curves
Abelian Group and Elliptic Curves
Discrete Logarithm Problem (DLP)
Generators and Cyclic Subgroups
tinyec - Python Library for ECC
ECDH (Elliptic Curve Diffie-Hellman) Key Exchange
ECDSA (Elliptic Curve Digital Signature Algorithm)