Physics Notes - Herong's Tutorial Notes - v3.25, by Herong Yang
Demonstration of Time Dilation - Formula
This section continues the thought experiment to demonstrate time dilation. An isosceles triangle is used to derive the time dilation formula with Lorentz factor.
Part 3 - Time Dilation Formula: The third part of the thought experiment is to derive the time dilation formula using the Pythagorean theorem. This part consists of the following:
1. Establish an isosceles triangle with trajectories of the laser meter and light pulse in Bob's frame:
- The trajectory of the laser meter forms the base of the isosceles triangle, D.
- The trajectory of the light pulse forms two legs of the isosceles triangle, L' and L'.
2. Establish a relation between the leg length L and L' based on the Pythagorean theorem:
L'**2 = D**2 + L**2 (T.9) - Pythagorean theorem 2*D = v*T' (T.10) - maser meter moves at speed v L'**2 = (v*T'/2)**2 + L**2 (T.11) - merging T.10 into T.9
3. Calculate time dilation factor:
2*L = c*T (T.1) - Amy's observation 2*L' = c*T' (T.3) - Bob's observation L'**2 = (v*T'/2)**2 + (c*T/2)**2 (T.12) - merging T.1 into T.11 4*L'**2 = (v*T')**2 + (c*T)**2 (T.13) - multiplying by 4 4*(c*T'/2)**2 = (v*T')**2 + (c*T)**2 (T.14) - merging T.3 into T.13 (c*T')**2 = (v*T')**2 + (c*T)**2 (T.15) - simplifying left side (c*T')**2 - (v*T')**2 = (c*T)**2 (T.16) - moving T' terms together (c**2-v**2)*T'**2 = (c*T)**2 (T.17) - factoring T' sqrt(c**2-v**2)*T' = c*T (T.18) - taking square root T' = (c/sqrt(c**2-v**2))*T (T.19) - normalizing on T' T' = (1/sqrt(1-(v/c)**2))*T (T.20) - moving c into sqrt() # Time dilation formula
Voila! We derived the dilation formula. Bob's observed that Amy's bouncing light pulse clock is slower by a factor of (1/sqrt(1-(v/c)**2)), which is called Lorentz Factor (named after Hendrik Lorentz).
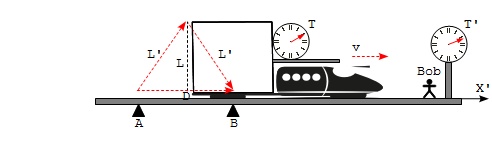
Table of Contents
Introduction of Frame of Reference
Introduction of Special Relativity
►Time Dilation in Special Relativity
Time Dilation - Moving Clock Is Slower
Demonstration of Time Dilation - Amy on the Train
Demonstration of Time Dilation - Bob on the Ground
►Demonstration of Time Dilation - Formula
Elapsed Time between Distant Events
Length Contraction in Special Relativity
The Relativity of Simultaneity
Minkowski Spacetime and Diagrams
Introduction of Generalized Coordinates