EC Cryptography Tutorials - Herong's Tutorial Examples - v1.03, by Herong Yang
EC Private Key Example - secp256k1
This section describes the elliptic curve, E(0,7), also named as secp256k1, and the subgroup parameters, which are used in Bitcoin, Ethereum, and many other cryptocurrency apps.
Now let's look at a good example of using EC (Elliptic Curve) private and public key pairs in real software applications as mentioned in "What is the math behind elliptic curve cryptography?" by Hans Knutson at hackernoon.com/what-is-the-math-behind-elliptic-curve-cryptography-f61b25253da3.
Bitcoin, Ethereum, and many other cryptocurrency apps use an elliptic curve called secp256k1:
Named elliptic curve: secp256k1
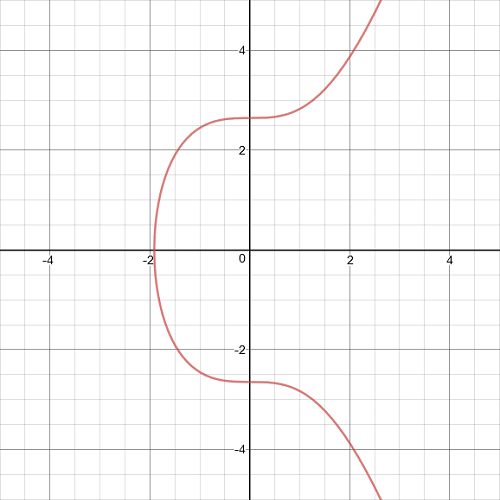
y2 = x3 + 7
The diagram below shows the elliptic curve, secp256k1, in the real number space:
Bitcoin, Ethereum, and many other cryptocurrency apps actually use the subgroup defined by the following parameters in hexadecimal format. See "Elliptic Curve Cryptography: ECDH and ECDSA" by Andrea Corbellini at andrea.corbellini.name/2015/05/30/elliptic-curve-cryptography-ecdh-and-ecdsa/.
p = 0xfffffffffffffffffffffffffffffffffffffffffffffffffffffffefffffc2f
a = 0
b = 7
G = (0x79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798,
0x483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8)
n = 0xfffffffffffffffffffffffffffffffebaaedce6af48a03bbfd25e8cd0364141
h = 1
Andrea Corbellini also shared Python script, ecdhe.py, to generate a private and public key pair for Alice:
herong> python ecdhe.py Curve: secp256k1 Alice's private key: 0xc2cdf0a8b0a83b35ace53f097b5e6e6a0a1f2d40535eff1cf434f52a43d59d8f Alice's public key: (0x6fcc37ea5e9e09fec6c83e5fbd7a745e3eee81d16ebd861c9e66f55518c19798, 0x4e9f113c07f875691df8afc1029496fc4cb9509b39dcd38f251a83359cc8b4f7)
By the way, the named curve, secp256k1, refers to the elliptic curve, E(0,7), and those subgroup parameters together as EC domain parameters.
Table of Contents
Geometric Introduction to Elliptic Curves
Algebraic Introduction to Elliptic Curves
Abelian Group and Elliptic Curves
Discrete Logarithm Problem (DLP)
Generators and Cyclic Subgroups
tinyec - Python Library for ECC
EC Private and Public Key Pair
►EC Private Key Example - secp256k1
Generate secp256k1 Keys with OpenSSL
ECDH (Elliptic Curve Diffie-Hellman) Key Exchange
ECDSA (Elliptic Curve Digital Signature Algorithm)