Physics Notes - Herong's Tutorial Notes

∟Introduction of Generalized Coordinates

∟Generalized Coordinates and Generalized Velocity

This section provides a quick introduction to the Generalized Coordinates and Generalized Velocity.

What are Generalized Coordinates? Generalized Coordinates are independent functions q_i(t), that can be used to represent positions in Cartesian coordinates through a set of transformation functions.

q(t) = (q1(t), q2(t), q3(t))
  # Generalized coordinates

r(t) = (rx(t), ry(t), rz(t))
  # Cartesian coordinates

r(t) = (r1(q1(t), q2(t), q3(t)),
       (r2(q1(t), q2(t), q3(t)),
       (r3(q1(t), q2(t), q3(t)))
  # r1(), r2(), and r3() are transformation functions

or:
  r(t) = r(q(t))                  (C.1)

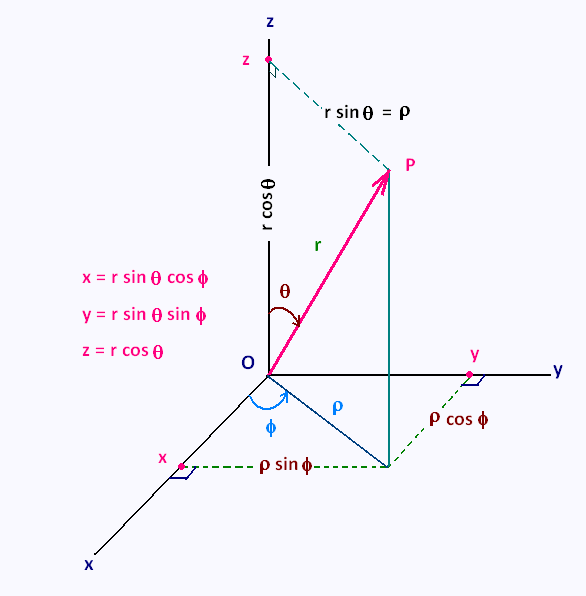
The diagram below shows the spherical coordinates as an example of generalized coordinates (source: quora.com)

What Is Generalized Velocity? Generalized Velocity is a vector of time derivatives of generalized coordinates.

q'(t) = (dq1/dt, dq2/dt, dq3/dt)

The velocity in Cartesian coordinates can be expressed in generalized velocity through transformation functions:

r'(t) = d(r(q(t))) / dt

r'(t) = (∑ ∂r1/∂qi * dqi/dt,
         ∑ ∂r2/∂qi * dqi/dt,
         ∑ ∂r3/∂qi * dqi/dt)
  # The chain rule for derivatives applied

or:
  r'(t) = (∂r1/∂q ∙ dq/dt,
           ∂r2/∂q ∙ dq/dt,
           ∂r3/∂q ∙ dq/dt)
  # Dot product operation applied

or:
  r'(t) = ∂r/∂q ∙ dq/dt

or:
  r' = ∂r/∂q ∙ q'                 (C.2)

Table of Contents

 About This Book

 Introduction of Space

 Introduction of Frame of Reference

 Introduction of Time

 Introduction of Speed

 Newton's Laws of Motion

 Introduction of Special Relativity

 Time Dilation in Special Relativity

 Length Contraction in Special Relativity

 The Relativity of Simultaneity

 Introduction of Spacetime

 Minkowski Spacetime and Diagrams

 Introduction of Hamiltonian

 Introduction of Lagrangian

►Introduction of Generalized Coordinates

►Generalized Coordinates and Generalized Velocity

 Simple Pendulum Motion in Generalized Coordinates

 Hamilton's Principle in Generalized Coordinates

 Lagrange Equations in Generalized Coordinates

 Lagrange Equations on Simple Pendulum

 What Is Generalized Momentum

 What Is Legendre Transformation

 Hamilton Equations in Generalized Coordinates

 Phase Space and Phase Portrait

 References

 Full Version in PDF/ePUB

Generalized Coordinates and Generalized Velocity - Updated in 2022, by Herong Yang