Physics Notes - Herong's Tutorial Notes - v3.24, by Herong Yang
Lagrange Equations on Simple Pendulum
This section provides an example of applying the Lagrange Equations on an object in simple pendulum motion using generalized coordinates.
What Is Simple Pendulum Motion? A Simple Pendulum Motion is an object of mass m hanging on a string from a pivot point so that it is constrained to move on a circle of radius L.
Let's introduce 2 generalized coordinates to describe this motion, θ and l:
q = (θ, l) where: # θ is the angular position from the vertical line # l is the length of the string
The transformation functions are:
r = (x, y)
r = (r1(), r2())
r = (l*sin(θ), -l*cos(θ))
Then the velocity is:
r' = dr/dt
or:
r' = (l*cos(θ)*θ', l*sin(θ)*θ')
Then the kinetic energy is:
T = m*v*v/2 or: T = 0.5*m*r'*r' or: T = 0.5*m*l*l*(cos(θ)**2)+sin(θ)**2)*θ'*θ' or: T = 0.5*m*l*l*θ'*θ' # Since cos(θ)**2)+sin(θ)**2 = 1
Then the potential energy is:
V = m*g*y or: V = m*g*(-l*cos(θ)) or: V = -m*g*l*cos(θ)
The Lagrangian function in generalized coordinates becomes:
L = T - V (G.1)
or:
L = 0.5*m*l*l*θ'*θ' + m*g*l*cos(θ)
Now take the Lagrange Equations in generalized coordinates:
d(∂L/∂q')/dt = ∂L/∂q (C.3) or: d(∂L/∂θ')/dt = ∂L/∂θ d(∂L/∂l')/dt = ∂L/∂l or: d(m*l*l*θ')/dt = -m*g*l*sin(θ) 0 = 0 or: m*l*l*θ" = -m*g*l*sin(θ) or: l*θ" = -g*sin(θ)
Wow! It is much easier to use generalized coordinates than Cartesian coordinates in this case.
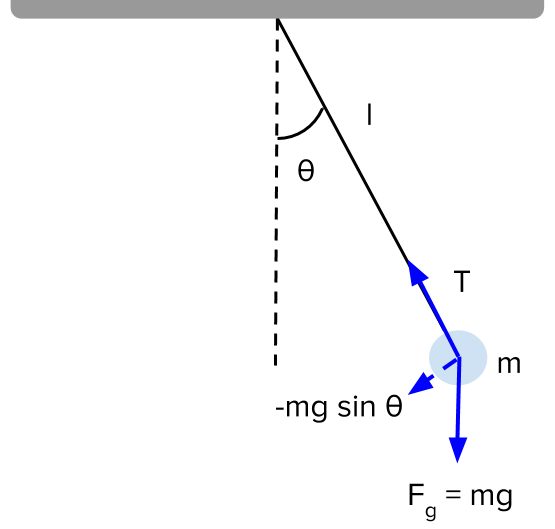
Table of Contents
Introduction of Frame of Reference
Introduction of Special Relativity
Time Dilation in Special Relativity
Length Contraction in Special Relativity
The Relativity of Simultaneity
Minkowski Spacetime and Diagrams
►Introduction of Generalized Coordinates
Generalized Coordinates and Generalized Velocity
Simple Pendulum Motion in Generalized Coordinates
Hamilton's Principle in Generalized Coordinates
Lagrange Equations in Generalized Coordinates
►Lagrange Equations on Simple Pendulum
What Is Legendre Transformation
Hamilton Equations in Generalized Coordinates