EC Cryptography Tutorials - Herong's Tutorial Examples

∟Algebraic Introduction to Elliptic Curves

∟Elliptic Curves with Singularities

This section describes elliptic curves with singularities where curves are not smooth.

If we review the elliptic curve equation again, we will see that for certain combination of coefficients a and b, the elliptic curve will have a singularity point where the curve is not smooth. 

y2 = x3 + ax + b

Here are two examples of elliptic curves with singularities (source: andrea.corbellini.name):

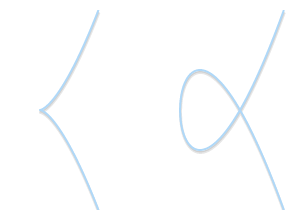
Elliptic Curve with Singularities
Elliptic Curves with Singularities

To exclude curves with singularities, we need to add an extra condition on coefficients a and b: 

y2 = x3 + ax + b
4a3 + 27b2 != 0

Table of Contents

 About This Book

 Geometric Introduction to Elliptic Curves

►Algebraic Introduction to Elliptic Curves

 Algebraic Description of Elliptic Curve Addition

 Algebraic Solution for Symmetrical Points

 Algebraic Solution for the Infinity Point

 Algebraic Solution for Point Doubling

 Algebraic Solution for Distinct Points

►Elliptic Curves with Singularities

 Elliptic Curve Point Addition Example

 Elliptic Curve Point Doubling Example

 Abelian Group and Elliptic Curves

 Discrete Logarithm Problem (DLP)

 Finite Fields

 Generators and Cyclic Subgroups

 Reduced Elliptic Curve Groups

 Elliptic Curve Subgroups

 tinyec - Python Library for ECC

 EC (Elliptic Curve) Key Pair

 ECDH (Elliptic Curve Diffie-Hellman) Key Exchange

 ECDSA (Elliptic Curve Digital Signature Algorithm)

 ECES (Elliptic Curve Encryption Scheme)

 EC Cryptography in Java

 Standard Elliptic Curves

 Terminology

 References

 Full Version in PDF/EPUB