EC Cryptography Tutorials - Herong's Tutorial Examples

∟Generators and Cyclic Subgroups

∟What Is Cyclic Group

This section describes Cyclic Group, which is a finite Abelian group that can be generated by a single element using the scalar multiplication operation in additive notation (or exponentiation operation in multiplicative notation).

What Is Cyclic Group? A Cyclic Subgroup is a finite Abelian group that can be generated by a single element using the scalar multiplication operation in additive notation (or exponentiation operation in multiplicative notation).

A Cyclic Group can be expressed in additive notation as: 

A finite Abelian Group is a Cyclic Group,
if it's elements can be expressed as:
   {P, P+P, P+P+P, ..., P+P+...+P} or
   {P, 2P, 3P, ..., nP}, where n is the order of the group
   nP = 0 is the identity element

A Cyclic Group can be expressed in multiplicative notation as: 

A finite Abelian Group is a Cyclic Group,
if it's elements can be expressed as:
   {P, P*P, P*P*P, ..., P*P*...*P} or
   {P, P2, P3, ..., Pn}, where n is the order of the group
   Pn = 1 is the identity element

Cyclic Group Example 1 - Here is a Cyclic group of integers: 0, 3, 6, 9, 12, 15, 18, 21 and the addition operation with modular reduction of 24. Integer 3 is a group generator: 

P = 3
2P = 6
3P = 9
4P = 12
5P = 15
6P = 18
7P = 21
8P = 0

Cyclic Group Example 2 - Here is a Cyclic group of polynomials: 0, x+1, 2x+2, and the algebraic addition operation with modular reduction of 3 on coefficients. Polynomial x+1 is a group generator: 

P = x+1
2P = 2x+2
3P = 0

Cyclic Group Example 3 - Here is a Cyclic group of integers: 1, 3, 4, 5, 9, and the multiplication operation with modular reduction of 11. Integer 3 is a group generator: 

P = 3
P2 = 9
P3 = 27 = 5, (mod 11)
P4 = 81 = 4, (mod 11)
P5 = 243 = 1, (mod 11)

Cyclic Group Example 4 - Here is a Cyclic group of integers: 1, 2, 3, 4, 5, 6, and the multiplication operation with modular reduction of 7. Integer 3 is a group generator: 

P = 3
P2 = 9 = 2, (mod 7)
P3 = 27 = 6, (mod 7)
P4 = 81 = 4, (mod 7)
P5 = 243 = 5, (mod 7)
P6 = 729 = 1, (mod 7)

If express P6 as P0 in the last example and replace P with Z, we can use the following graph to represent this Cyclic Group:

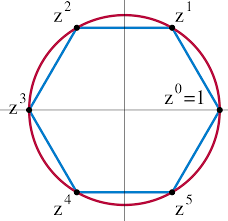
Graph of Cyclic Group with Order of 6
Graph of Cyclic Group with Order of 6

Table of Contents

 About This Book

 Geometric Introduction to Elliptic Curves

 Algebraic Introduction to Elliptic Curves

 Abelian Group and Elliptic Curves

 Discrete Logarithm Problem (DLP)

 Finite Fields

►Generators and Cyclic Subgroups

 What Is Subgroup in Abelian Group

 What Is Subgroup Generator in Abelian Group

 What Is Order of Element

 Every Element Is Subgroup Generator

 Order of Subgroup and Lagrange Theorem

►What Is Cyclic Group

 Element Generated Subgroup Is Cyclic

 Reduced Elliptic Curve Groups

 Elliptic Curve Subgroups

 tinyec - Python Library for ECC

 EC (Elliptic Curve) Key Pair

 ECDH (Elliptic Curve Diffie-Hellman) Key Exchange

 ECDSA (Elliptic Curve Digital Signature Algorithm)

 ECES (Elliptic Curve Encryption Scheme)

 EC Cryptography in Java

 Standard Elliptic Curves

 Terminology

 References

 Full Version in PDF/EPUB