EC Cryptography Tutorials - Herong's Tutorial Examples

∟Algebraic Introduction to Elliptic Curves

∟Algebraic Description of Elliptic Curve Addition

This section provides an algebraic description of the problem of calculating the addition operation defined on an elliptic curve.

In the previous chapter, we have discussed elliptic curves and an "addition" operation from a geometric point of view. In this chapter, let's look at them from an algebraic point of view. This should help us calculate the "addition" operation using algebraic formulas.

First, let's describe the "addition" operation problem in algebraic terms:

For a given elliptic curve represented as:
   y2 = x3 + ax + b

And two given points on the curve represented as:
   P = (xP, yP)
   Q = (xQ, yQ)

Find a third point on the curved represented as:
   R = (xR, yR)

So that R is the result of the addition operation
of P and Q as defined by our geometrical algorithm:
   R = P + Q

Here is a diagram that illustrates how to perform the point addition operation on an elliptic curve geometrically (source: stackoverflow.com):

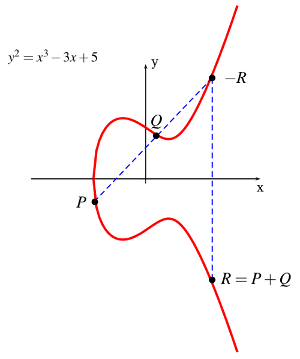
It will be easier to find the algebraic solution, if we divide the problem into multiple cases:

• Case 1: P and Q are symmetrical points.
• Case 2: P or Q is the infinity point.
• Case 3: P and Q are the same point.
• Case 4: P and Q are two distinct points.

See next tutorials on algebraic solutions for those cases.

Table of Contents

 About This Book

 Geometric Introduction to Elliptic Curves

►Algebraic Introduction to Elliptic Curves

►Algebraic Description of Elliptic Curve Addition

 Algebraic Solution for Symmetrical Points

 Algebraic Solution for the Infinity Point

 Algebraic Solution for Point Doubling

 Algebraic Solution for Distinct Points

 Elliptic Curves with Singularities

 Elliptic Curve Point Addition Example

 Elliptic Curve Point Doubling Example

 Abelian Group and Elliptic Curves

 Discrete Logarithm Problem (DLP)

 Finite Fields

 Generators and Cyclic Subgroups

 Reduced Elliptic Curve Groups

 Elliptic Curve Subgroups

 tinyec - Python Library for ECC

 EC (Elliptic Curve) Key Pair

 ECDH (Elliptic Curve Diffie-Hellman) Key Exchange

 ECDSA (Elliptic Curve Digital Signature Algorithm)

 ECES (Elliptic Curve Encryption Scheme)

 EC Cryptography in Java

 Standard Elliptic Curves

 Terminology

 References

 Full Version in PDF/EPUB

Algebraic Description of Elliptic Curve Addition - Updated in 2024, by Herong Yang