Physics Notes - Herong's Tutorial Notes - v3.25, by Herong Yang
What Is an Inertial Frame of Reference
This section describes an inertial frame of reference - a frame of reference in which no acceleration can be detected in any direction.
What Is an Inertial Frame of Reference? An inertial frame of reference (or inertial frame) is a frame of reference in which no acceleration can be detected in any direction.
An inertial frame can be viewed as a spaceship cruising in the deep space far away from any stars with no power.
It is actually very hard to define an inertial frame without using another frame of reference. But we can easily define all inertial frames as a group: "All inertial frames are in a state of motion with a constant speed in a straight line".
In other words, when an observer in an inertial frame K views another inertial frame K', K' is moving away from K with a constant speed in a straight line, or K' is moving in uniform translation relatively to K.
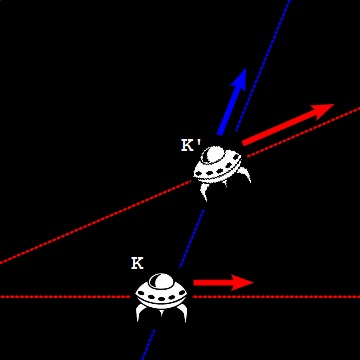
With the definition of inertial frames, now we can add a condition to the theory of special relativity that was not clearly mentioned in the previous section: "The theory of special relativity in valid only in inertial frames". And the two assumptions of the theory of special relativity can be restated as:
1. The Principle of Relativity - The laws of physics are the same in all inertial frames.
2. The Constancy of the Speed of Light - The speed of light has the same value c measured in all inertial frames.
Table of Contents
Introduction of Frame of Reference
►Introduction of Special Relativity
Assumptions of Special Relativity
►What Is an Inertial Frame of Reference
The Constancy of the Speed of Light
Time Dilation in Special Relativity
Length Contraction in Special Relativity
The Relativity of Simultaneity
Minkowski Spacetime and Diagrams
Introduction of Generalized Coordinates