Physics Notes - Herong's Tutorial Notes - v3.25, by Herong Yang
Meter Based on Earth's Meridian
This section introduces an old definition of 'meter' which uses the Paris meridian line. A 'meter' is about one ten-millionth of the length of a quadrant of the Paris meridian.
In year 1791, the French National Assembly accepted a definition of "meter" to be equal to one ten-millionth of the length of a quadrant of the Paris meridian.
This definition is based on the Paris meridian which is the meridian line running through the Paris Observatory in Paris, France, with a longitude of 2°20'14.03" east, very close to the Prime meridian (longitude 0°) running through Greenwich.
A quadrant of the Paris meridian is one fourth of the entire meridian length, or the length of the smaller segment between the Equator and the North Pole of the Paris meridian as shown in the picture below:
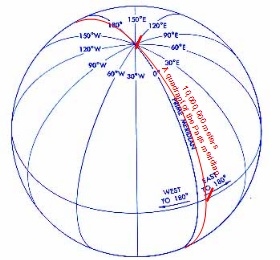
This definition of "meter" is very interesting. It tells us that a quadrant of the Paris meridian is ten million meters (10,000,000 meters) long. If you are running with an average of 1 meter per step, you have to run 10,000,000 steps from the Equator along the Paris meridian line at the see level to reach the North Pole.
It also tells us that the length of the entire Paris meridian is 40,000,000 meters. If we assume the Earth is perfectly symmetric, all meridian lines are 40,000,000 meters long.
Since "meter" is defined more accurately now with the speed of light, the accurate length of a median line is 40,007,860 meters.
If you are interested in the length of the Equator line, it is 40,075,000 meters. Earth is almost a perfect sphere with only about 70,000 meters longer in the Equator line.
Table of Contents
►Meter Based on Earth's Meridian
Meter Based on Seconds Pendulum
Meter Prefixes and Other Units
List of Various Distances and Lengths
Introduction of Frame of Reference
Introduction of Special Relativity
Time Dilation in Special Relativity
Length Contraction in Special Relativity
The Relativity of Simultaneity
Minkowski Spacetime and Diagrams
Introduction of Generalized Coordinates