Physics Notes - Herong's Tutorial Notes - v3.24, by Herong Yang
Demonstration of Time Dilation - Amy on the Train
This section provides a thought experiment to demonstrate time dilation by starting with Amy synchronizing a clock with a bouncing light pulse on a moving train.
The most common way to demonstrate time dilation is to follow a thought experiment using a clock on a train moving relative the ground.
Part 1 - Amy on the Train: The first part of the thought experiment is to synchronize the moving clock and a laser light pulse bouncing perpendicular to the moving direction of the clock. This part consists of the following:
- Amy stays on a train that is moving at a speed of v relative the ground.
- Amy carries a clock which is also moving along with the train at the speed of v meters per second.
- Amy installs a laser meter on the floor of the carriage on the train and a mirror on the ceiling of the carriage. The distance between the meter and mirror is L meters.
- Amy releases laser light pulses from the meter, and waits for pulses to be reflected back from the mirror.
- Amy observes that a light pulse always takes T seconds on her clock to finish a round trip from the meter, to the mirror, and back to the meter.
- Amy uses the train as her frame of reference x.
- Assuming the distance from the carriage floor to the ceiling is L meters, Amy observes that the light pulse travels twice the distance of L in her frame: one time going up from the meter to the mirror and one time going down from the mirror to the meter.
- Amy establishes a relation between the elapsed time of T seconds on her clock with the distance L meters using the speed of light c: 2*L = c*T.
- Amy declares that her clock is synchronized with the light pulse bouncing between the laser meter and the mirror. Each time her clock moves T seconds, the light pulse completes a single round trip of bouncing.
Based on Amy's observations in her frame, we can derive a formula to express time T in terms of distance L:
2*L = c*T (T.1) - Amy's observation # Light pulse speed, time and distance relation T = 2*L/c (T.2) - moving variables around # Time on the moving clock in Amy's frame
Notice that T also represents the elapsed time observed by Amy between two events: event A when the light pulse is leaving the meter, and event B when the same light pulse is returning to the meter reflected back from the mirror.
With Amy's clock synchronized with the bouncing light pulse, we can say that the bouncing light pulse itself is also a moving clock. It moves T seconds per click.
Now we are ready to measure the speed of time on the moving frame from a stationary frame by observing the elapsed time of between two clicks of the bouncing light pulse clock. Continue with the second part of the thought experiment in the next section.
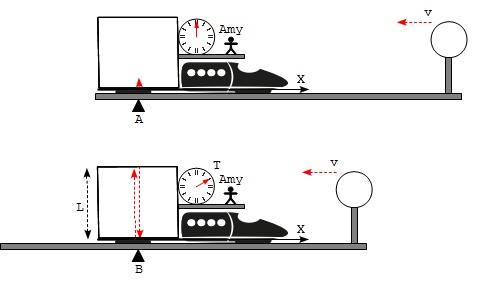
Table of Contents
Introduction of Frame of Reference
Introduction of Special Relativity
►Time Dilation in Special Relativity
Time Dilation - Moving Clock Is Slower
►Demonstration of Time Dilation - Amy on the Train
Demonstration of Time Dilation - Bob on the Ground
Demonstration of Time Dilation - Formula
Elapsed Time between Distant Events
Length Contraction in Special Relativity
The Relativity of Simultaneity
Minkowski Spacetime and Diagrams
Introduction of Generalized Coordinates