Reduced Elliptic Curve Group

EC Cryptography Tutorials - Herong's Tutorial Examples

∟Reduced Elliptic Curve Group - E97(-1,1)

This section provides an example of a reduced Elliptic Curve group E97(-1,1). Some example points on the curve are is also provided.

Let's take a look at our second reduced elliptic curve group, E₉₇(-1,1), as discussed in "A (relatively easy to understand) primer on elliptic curve cryptography" by Nick Sullivan at arstechnica.com/information-technology/2013/10 /a-relatively-easy-to-understand-primer-on-elliptic-curve-cryptography/2/.

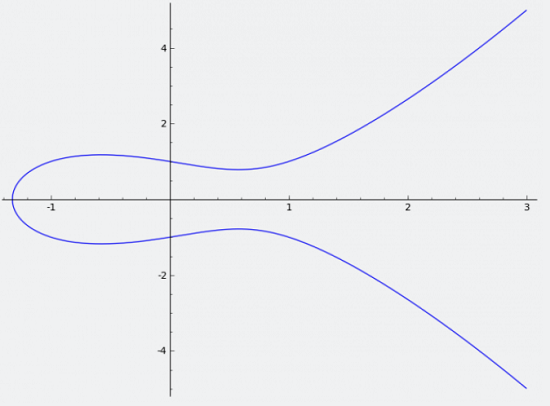
Here is the elliptic curve in the real number space:

   y² = x³ - x + 1

Elliptic Curve E(-1,1) in Real Number Space

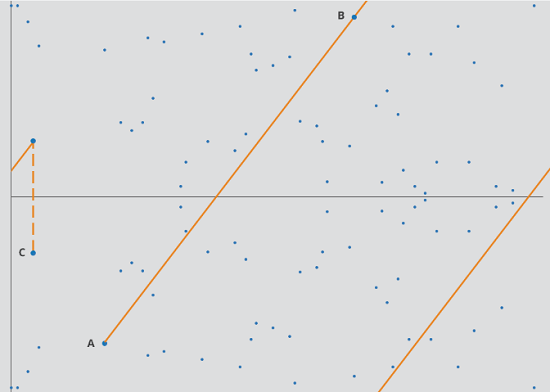
Here is the reduced elliptic curve group using modular arithmetic of prime number 97, E₉₇(-1,1):

   y² = x³ - x + 1 (mod 97)

Example points on the curve:

Verify (x,y) = (70,6) is on the curve:
   y² = x³ - x + 1 (mod 97)
   6*6 = 70*70*70 - 70 + 1 (mod 97)
   36 = 342931 (mod 97)
   36 = 36

Verify (x,y) = (76,48) is on the curve:
   y² = x³ - x + 1 (mod 97)
   48*48 = 76*76*76 - 76 + 1 (mod 97)
   2304 = 438901 (mod 97)
   73 = 73

Verify (x,y) = (82,6) is on the curve:
   y² = x³ - x + 1 (mod 97)
   6*6 = 82*82*82 - 82 + 1 (mod 97)
   36 = 551287 (mod 97)
   36 = 36

Verify (x,y) = (69,22) is on the curve:
   y² = x³ - x + 1 (mod 97)
   22*22 = 69*69*69 - 69 + 1 (mod 97)
   484 = 328441 (mod 97)
   96 = 96

An example of the addition operation using the rule of chord is also illustrated on the diagram presented above. But the straight line is wrapped around because of the modular arithmetic reduction:

Given two points on the curve:
   A = (17,12)
      12*12 = 17*17*17 - 17 + 1 (mod 97)
      144 = 4897 (mod 97)
      47 = 47
   B = (63,93)
      93*93 = 63*63*63 - 63 + 1 (mod 97)
      8649 = 249985 (mod 97)
      16 = 16

Draw a straight line passing through A and B,
And wrap the line around when it reaches the boundary of the region.
It will reach another point -C on the curve.
Take the symmetric point C of -C:
   C = A + B
   C = (4,35)
      35*35 = 4*4*4 - 4 + 1 (mod 97)
      1225 = 61 (mod 97)
      61 = 61

However, when I tried to calculate C = A+B using algebraic equations given by the reduced elliptic curve group definition, I got C = (89,51):

For any two given points on the curve:
   A = (x_P, y_P) = (17,12)
   B = (x_Q, y_Q) = (63,93)

C = A + B is a third point on the curve:
   C = (x_R, y_R)

Where:
   x_R = m² - x_P - x_Q (mod p)     (11)
   y_R = m(x_P - x_R) - y_P (mod p)  (12)
   m(x_P - x_Q) = y_P - y_Q (mod p)  (18)

Calculation:
   m*(17-63) = 12-93 (mod 97)
   m*(-46) = -81 (mod 97)
   51*m = 16 (mod 97)
   m = 16 * 1/51 (mod 97)
   m = 16 * 78 (mod 97)
   m = 1248 (mod 97)
   m = 84

   x_R = 84*84 - 17 - 63 = 6976 (mod 23)
   x_R = 89

   y_R = 86*(17 - 89) - 12 = -6060 (mod 23)
   y_R = 51

   C = (89,51)